以太坊创始人 Vitalik Buterin 解析 Binius:对二进制字段的高效证明
火星财经编译报道:在过去的两年中,STARK已成为一种关键且不可替代的技术,可以有效地对非常复杂的语句进行易于验证的加密证明(例如,证明以太坊区块是有效的)。
其中一个关键原因是字段大小:基于椭圆曲线的SNARK要求您在256位整数上工作才能足够安全,而STARK允许您使用更小的字段大小,效率更高:首先是Goldilocks字段(64位整数),然后是Mersenne31和BabyBear(均为31位)。由于这些效率的提高,使用Goldilocks的Plonky2在证明多种计算方面比其前辈快数百倍。
一个自然而然的问题是:我们能否将这一趋势引向合乎逻辑的结论,通过直接在零和一上操作来构建运行速度更快的证明系统?这正是Binius试图做的事情,使用了许多数学技巧,使其与三年前的SNARK和STARK截然不同。这篇文章介绍了为什么小字段使证明生成更有效率,为什么二进制字段具有独特的强大功能,以及Binius用来使二进制字段上的证明如此有效的技巧。

△ Binius。在这篇文章的最后,你应该能够理解此图的每个部分。
回顾:有限域(finite fields)
加密证明系统的关键任务之一是对大量数据进行操作,同时保持数字较小。如果你可以将一个关于大型程序的语句压缩成一个包含几个数字的数学方程,但是这些数字与原始程序一样大,那么你将一无所获。
为了在保持数字较小的情况下进行复杂的算术,密码学家通常使用模运算(modular arithmetic)。我们选择一个质数「模数」p。% 运算符的意思是「取余数」:15%7=1,53%10=3,等等。(请注意,答案总是非负数的,所以例如 -1%10=9)
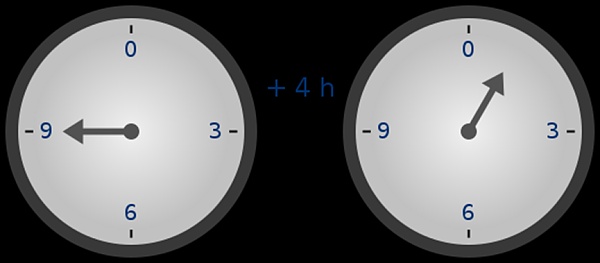
你可能已经在时间的加减上下文中见过模运算(例如,9点过4小时是几点?但在这里,我们不只是对某个数进行加、减模,我们还可以进行乘、除和取指数。
我们重新定义:

5+3=1(因为 8%7=1)
1-3=5(因为 -2%7=5)
2*5=3
3/5=2
这种结构的更通用术语是有限域。有限域是一种数学结构,它遵循通常的算术法则,但其中可能的值数量有限,因此每个值都可以用固定的大小表示。
模运算 ( 或质数域 ) 是有限域最常见的类型,但也有另一种类型:扩展域。你可能已经见过一个扩展字段:复数。我们「想象」一个新元素,并给它贴上标签 i,并用它进行数学运算:(3i+2)*(2i+4)=6i*i+12i+4i+8=16i+2。我们可以同样地取质数域的扩展。当我们开始处理较小的字段时,质数字段的扩展对于保护安全性变得越来越重要,而二进制字段 (Binius 使用 ) 完全依赖于扩展以具有实际效用。
回顾:算术化
SNARK 和 STARK 证明计算机程序的方法是通过算术:你把一个关于你想证明的程序的陈述,转换成一个包含多项式的数学方程。方程的有效解对应于程序的有效执行。
举个简单的例子,假设我计算了第 100 个斐波那契数,我想向你证明它是什么。我创建了一个编码斐波那契数列的多项式 F:所以 F(0)=F(1)=1、F(2)=2、F(3)=3、F(4)=5 依此类推,共 100 步。我需要证明的条件是 F(x+2)=F(x)+F(x+1) 在整个范围内 x={0,1…98}。我可以通过给你商数来说服你:
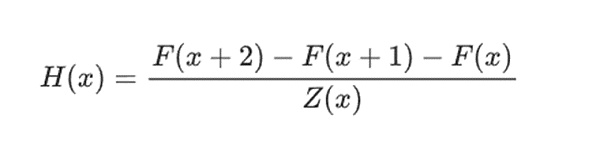
其中 Z(x) = (x-0) * (x-1) * …(x-98)。如果我能提供有 F 且 H 满足此等式,则 F 必须在该范围内满足 F(x+2)-F(x+1)-F(x)。如果我另外验证满足 F,F(0)=F(1)=1,那么 F(100) 实际上必须是第 100 个斐波那契数。
如果你想证明一些更复杂的东西,那么你用一个更复杂的方程替换「简单」关系 F(x+2) = F(x) + F(x+1),它基本上是说「F(x+1) 是初始化一个虚拟机的输出,状态是 F(x)」,并运行一个计算步骤。你也可以用一个更大的数字代替数字 100,例如,100000000,以容纳更多的步骤。
所有 SNARK 和 STARK 都基于这种想法,即使用多项式 ( 有时是向量和矩阵 ) 上的简单方程来表示单个值之间的大量关系。并非所有的算法都像上面那样检查相邻计算步骤之间的等价性:例如,PLONK 没有,R1CS 也没有。但是许多最有效的检查都是这样做的,因为多次执行相同的检查 ( 或相同的少数检查 ) 可以更轻松地将开销降至最低。
Plonky2:从 256 位 SNARK 和 STARK 到 64 位......只有 STARK
五年前,对不同类型的零知识证明的合理总结如下。有两种类型的证明:( 基于椭圆曲线的 )SNARK 和 ( 基于哈希的 )STARK。从技术上讲,STARK 是 SNARK 的一种,但在实践中,通常使用「SNARK」来指代基于椭圆曲线的变体,而使用「STARK」来指代基于哈希的结构。SNARK 很小,因此你可以非常快速地验证它们并轻松地将它们安装在链上。STARK 很大,但它们不需要可信的设置,而且它们是抗量子的。

STARK:下一代零知识证明技术
It has become the key to the easy-to-verify encryption proof of very complex sentences. The Mars financial compilation report has become a key and irreplaceable technology in the past two years, which can effectively prove the easy-to-verify encryption proof of very complex sentences, for example, proving that the Ethereum block is effective. One of the key reasons is that the field size is based on the elliptic curve, so that you can work on the bit integer safely enough and allow you to use a smaller field size. First of all, the field bit integer is more efficient. Because of these improvements in efficiency, numbers and sums are hundreds of times faster than their predecessors in proving a variety of calculations. A natural question is whether we can lead this trend to a logical conclusion and build a faster proof system by operating directly on zero and one. This is exactly what we are trying to do, using many mathematical skills to make it completely different from that of three years ago. This article introduces why small fields make proof generation more efficient and why binary fields are available. At the end of this article, you should be able to understand every part of this figure. One of the key tasks of the finite field encryption proof system is to operate on a large amount of data while keeping the numbers small. If you can compress a statement about a large program into a mathematical equation containing several numbers, but these numbers are as big as the original program, then you will get nothing in order to keep the numbers small. In the case of complex arithmetic cryptographers usually use modular operation. We choose a prime modular operator, which means to take the remainder, etc. Please note that the answer is always non-negative, so for example, you may have seen modular operation in the context of adding and subtracting time, for example, what time is it when the hour is too small, but here we can not only add and subtract a certain number, but also multiply, divide and take the exponent. It is quite interesting to redefine the calculation according to the above rules, for example, because of this assumption. The more general term of structure is finite field, which is a mathematical structure. It follows the usual arithmetic rules, but the number of possible values is limited, so each value can be represented by a fixed size. Modular operation or prime number field is the most common type of finite field, but there is another type of extension field. You may have seen an extension field complex number. We imagine a new element and label it and use it for mathematical operation. We can also take the extension of prime number field when we start to deal with smaller ones. The extension of prime number field is becoming more and more important for protecting security, and the use of binary field depends entirely on extension to have practical utility. The way to review arithmetics and prove computer programs is through arithmetic. You transform a statement about the program you want to prove into an effective solution of a mathematical equation containing polynomials, which corresponds to the effective execution of the program. Let's give a simple example. Suppose I calculate the first Fibonacci number and I want to prove to you what it is. I created a compilation. Polynomial of code Fibonacci sequence, so the condition that I need to prove is that I can convince you by giving you quotient in the whole range, in which if I can provide existence and satisfy this equation, it must be satisfied within this range. If I verify that it is satisfied, it must actually be the first Fibonacci number. If you want to prove something more complicated, then you can replace the simple relationship with a more complicated equation, which basically means that the output state of initializing a virtual machine is parallel. For each calculation step, you can also use a larger number instead of a number, for example, to accommodate more steps. All sums are based on the idea that polynomials, sometimes simple equations on vectors and matrices, are used to represent a large number of relationships between single values. Not all algorithms check the equivalence between adjacent calculation steps like the above, for example, none, but many of the most effective checks are done because it is easier to perform the same check or the same few checks many times. Minimize the overhead. Only five years ago, a reasonable summary of different types of zero-knowledge proofs was made. There are two types of proofs as follows: elliptic curve-based proof and hash-based proof. Technically, they are one, but in practice, they are usually used to refer to variants based on elliptic curves, while hash-based structures are very small, so you can verify them very quickly and easily install them on the chain. They are very large, but they don't need credible settings, and they are the next generation of anti-quantum zero-knowledge proof technology. 比特币今日价格行情网_okx交易所app_永续合约_比特币怎么买卖交易_虚拟币交易所平台
STARK(Scalable Transparent ARguments of Knowledge)是一种创新的零知识证明技术,其工作原理是将数据视为多项式,并计算该多项式的计算。使用扩展数据的默克尔根作为「多项式承诺」,STARK 实现了高效的零知识证明。
一个关键的历史节点是,基于椭圆曲线的SNARK(Succinct Non-interactive ARguments of Knowledge)首先得到了广泛的使用。直到2018年左右,STARK才变得足够高效,这要归功于FRI(Fast Reed-Solomon Interactive Oracle Prover),而那时Zcash已经运行了一年多。
基于椭圆曲线的SNARK有一个关键的限制:如果要使用基于椭圆曲线的SNARK,那么这些方程中的算术必须使用椭圆曲线上的点数模数来完成。然而,实际的计算使用的是小数字,例如计数器、for循环中的索引、程序中的位置等,这些通常只有几位数长。
即使原始数据由小数字组成,证明过程也需要进行计算商数、扩展、随机线性组合和其他数据转换,这将导致相等或更大数量的对象,这些对象的平均大小与你的字段的全部大小一样大。这造成了一个关键的低效率:为了证明对n个小值的计算,你必须对n个大得多的值进行更多的计算。起初,STARK 继承了SNARK使用256位字段的习惯,因此也遭受了同样的低效率。

Plonky2发布
2022 年,Plonky2 发布。Plonky2 的主要创新是对一个较小的质数进行算术取模:2 的 64 次方 – 2 的 32 次方 + 1 = 18446744067414584321。现在,每次加法或乘法总是可以在 CPU 上的几个指令中完成,并且将所有数据哈希在一起的速度比以前快 4 倍。但这有一个问题:这种方法只适用于 STARK。如果你尝试使用 SNARK,对于如此小的椭圆曲线,椭圆曲线将变得不安全。
为了保证安全,Plonky2 还需要引入扩展字段。检查算术方程的一个关键技术是「随机点抽样」:如果你想检查的 H(x) * Z(x) 是否等于 F(x+2)-F(x+1)-F(x),你可以随机选择一个坐标 r,提供多项式承诺开证明证明 H(r)、Z(r) 、F(r),F(r+1) 和 F(r+2),然后进行验证 H(r) * Z(r) 是否等于 F(r+2)-F(r+1)- F(r)。如果攻击者可以提前猜出坐标,那么攻击者就可以欺骗证明系统——这就是为什么证明系统必须是随机的。但这也意味着坐标必须从一个足够大的集合中采样,以使攻击者无法随机猜测。如果模数接近 2 的 256 次方,这显然是事实。但是,对于模数量是 2 的 64 次方 -2 的 32 次方 +1,我们还没到那一步,如果我们降到 2 的 31 次方 -1,情况肯定不是这样。试图伪造证明 20 亿次,直到一个人幸运,这绝对在攻击者的能力范围内。
为了阻止这种情况,我们从扩展字段中采样 r,例如,你可以定义 y,其中 y 的 3 次方=5,并采用 1、y、y 的 2 次方的组合。这将使坐标的总数增加到大约 2 的 93 次方。证明者计算的多项式的大部分不进入这个扩展域;只是用整数取模 2 的 31 次方 -1,因此,你仍然可以从使用小域中获得所有的效率。但是随机点检查和 FRI 计算确实深入到这个更大的领域,以获得所需的安全性。
从小质数到二进制数
计算机通过将较大的数字表示为 0 和 1 的序列来进行算术运算,并在这些 bit 之上构建「电路」来计算加法和乘法等运算。计算机特别针对 16 位、32 位和 64 位整数进行了优化。例如,2 的 64 次方 -2 的 32 次方 +1 和 2 的 31 次方 -1,选择它们不仅是因为它们符合这些界限,还因为它们与这些界限很吻合:可以通过执行常规的 32 位乘法来执行乘法取模 2 的 64 次方 -2 的 32 次方 +1,并在几个地方按位移位和复制输出;这个文章很好地解释了一些技巧。
然而,更好的方法是直接用二进制进行计算。如果加法可以「只是」异或,而无需担心「携带」从一个位添加 1 + 1 到下一个位的溢出?如果乘法可以以同样的方式更加并行化呢?这些优点都是基于能够用一个 bit 表示真 / 假值。
获取直接进行二进制计算的这些优点正是 Binius 试图做的。Binius 团队在 zkSummit 的演讲中展示了效率提升:
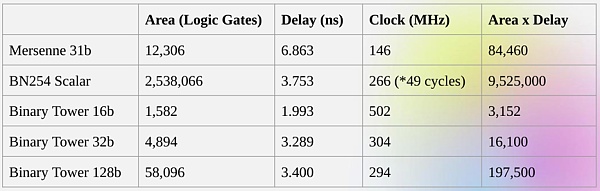
一些多项式求值的 Reed-Solomon 扩展。尽管原始值很小,但额外的值都将扩展到字段的完整大小 ( 在本例中是 2 的 31 次方 -1)
```html
近日有重要发现,32位二进制字段操作与31位 Mersenne 字段操作相比,所需计算资源减少了五倍,尽管二者的大小大致相同。
从一元多项式到超立方体
假设我们相信这一推理,并希望通过比特(0和1)来完成所有操作。那么,如何用一个多项式表示十亿比特呢?
在这方面,我们面临两个实际问题:
大量值的多项式表示中,这些值在多项式求值时需要被访问:在斐波那契数列的例子中,F(0),F(1) … F(100),在更大的计算中,指数可能会达到数百万。我们所使用的字段需要包含到这一范围的数字。
证明我们在 Merkle 树中提交的任何值(就像所有 STARK 一样)都需要经过 Reed-Solomon 编码:例如,将值从 n 扩展到 8n,使用冗余以防止恶意证明者通过在计算过程中伪造一个值来作弊。这也需要一个足够大的字段:要将一百万个值扩展到八百万个,你需要八百万个不同的点来计算多项式。
Binius 协议的一个关键思想是分别解决这两个问题,并通过以两种不同的方式表示相同的数据来实现。首先,是多项式本身。
基于椭圆曲线的 SNARK、2019 年的 STARK、Plonky2 等系统通常处理一个变量上的多项式:F(x)。而 Binius 则从 Spartan 协议中获得灵感,采用多元多项式:F(x1,x2,… xk)。实际上,我们在计算的“超立方体”上表示整个计算轨迹,其中每个 xi 不是 0 就是 1。例如,如果我们想要表示斐波那契数列,并且仍然使用足够大的字段来表示它们,我们可以将它们的前 16 个数列想象成这样:

也就是说,F(0,0,0,0) 应该是 1,F(1,0,0,0) 也是 1,F(0,1,0,0) 是 2,依此类推,一直到 F(1,1,1,1)=987。给定这样一个计算的超立方体,就会有一个产生这些计算的多元线性(每个变量的次数为 1)多项式。因此,我们可以将这组值视为多项式的代表;我们不需要计算系数。
这个例子当然只是为了说明:在实践中,进入超立方体的全部意义是让我们处理单个比特。计算斐波那契数的“Binius 原生”方法是使用一个高维的立方体,使用每组例如 16 位存储一个数字。这需要一些智慧来在比特基础上实现整数相加,但对于 Binius 来说,这并不太难。
现在,让我们来看看纠删码。STARK 的工作方式是:你取 n 值,Reed-Solomon 将它们扩展到更多的值(通常为 8n,通常在 2n 和 32n 之间),然后从扩展中随机选择一些 Merkle 分支,并对它们执行某种检查。超立方体在每个维度上的长度为 2。因此,直接扩展它是不切实际的:没有足够的“空间”从 16 个值中采样 Merkle 分支。那么我们该怎么做呢?我们假设超立方体是一个正方形!
简单的 Binius - 一个例子
有关该协议的 Python 实现,请复制下方链接到浏览器查阅:https://github.com/ethereum/research/blob/master/binius/simple_binius.
``````html让我们来看一个示例,为了方便起见,我们使用正则整数作为我们的字段(在实际实现中,将使用二进制字段元素)。首先,我们将想要提交的超立方体编码为正方形:
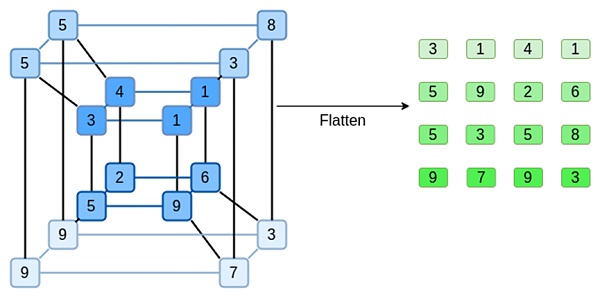
现在,我们用Reed-Solomon扩展正方形。也就是说,我们将每一行视为在x={0,1,2,3}处求值的3次多项式,并在x={4,5,6,7}处求值相同的多项式:

注意,数字会迅速膨胀!这就是为什么在实际实现中,我们总是使用有限域,而不是正则整数:如果我们使用整数模11,例如,第一行的扩展将只是[3,10,0,6]。
如果您想尝试扩展并亲自验证这里的数字,可以在这里使用我的简单Reed-Solomon扩展代码。
接下来,我们将此扩展视为列,并创建列的Merkle树。Merkle树的根是我们的承诺。
现在,让我们假设证明者想要在某个时候证明这个多项式的计算r={r0,r1,r2,r3}。在Binius中有一个细微的差别,使它比其他多项式承诺方案更弱:证明者在提交到Merkle根之前不应该知道或能够猜测s(换句话说,r应该是一个依赖于Merkle根的伪随机值)。这使得该方案对“数据库查找”无用(例如,“好吧,你给了我Merkle根,现在证明给我看P(0,0,1,0)”!)。
但是我们实际使用的零知识证明协议通常不需要“数据库查找”;他们只需要在一个随机的求值点检查多项式。因此,这个限制符合我们的目的。
假设我们选择r={1,2,3,4}(此时多项式的计算结果为-137;您可以使用此代码进行确认)。现在,我们进入了证明的过程。我们分为r两部分:第一部分{1,2}表示行内列的线性组合,第二部分{3,4}表示行的线性组合。我们计算一个“张量积”,对于列部分:
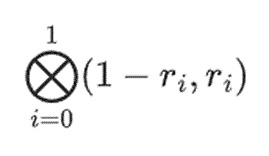
对于行部分:

这意味着:每个集合中一个值的所有可能乘积的列表。在行情况下,我们得到:
[(1-r2)*(1-r3), (1-r3), (1-r2)*r3, r2*r3]
使用r={1,2,3,4}(所以r2=3和r3=4):
[(1-3)*(1-4), 3*(1-4),(1-3)*4,3*4] = [6, -9, -8, -12]
现在,我们通过采用现有行的线性组合来计算一个新的“行”t。也就是说,我们取:
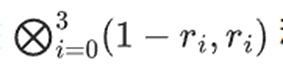
证明者向验证者提供以下新行:t 以及一些随机抽样列的 Merkle 证明。在我们的说明性示例中,我们将让证明程序只提供最后一列;在现实生活中,证明者需要提供几十列来实现足够的安全性。
现在,我们利用 Reed-Solomon 代码的线性。我们使用的关键属性是:取一个 Reed-Solomon 扩展的线性组合得到与线性组合的 Reed-Solomon 扩展相同的结果。这种「顺序独立性」通常发生在两个操作都是线性的情况下。
验证者正在这样做。他们计算了 t,并计算与证明者之前计算的相同列的线性组合(但只计算证明者提供的列),并验证这两个过程是否给出相同的答案。
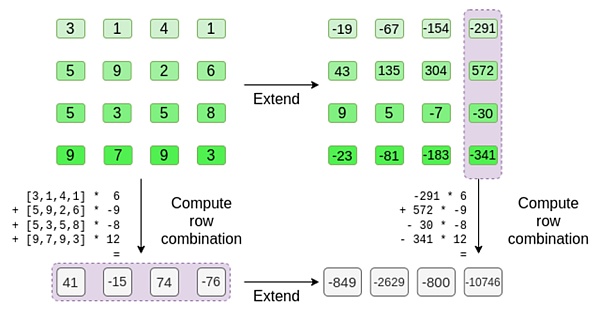
在本例中,扩展 t,计算相同的线性组合 ([6,-9,-8,12],两者给出了相同的答案:-10746。这证明默克尔的根是「善意」构建的(或至少「足够接近」),而且它是匹配 t 的:至少绝大多数列是相互兼容的。
但验证者还需要检查另一件事:检查多项式{r0…r3}的求值。到目前为止,验证者的所有步骤实际上都没有依赖于证明者声称的值。我们是这样检查的。我们取我们标记为计算点的「列部分」的张量积:
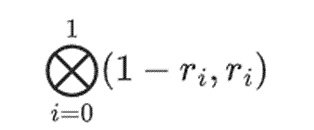
在我们的例子中,其中 r={1,2,3,4} 所以选择列的那一半是{1,2}),这等于:
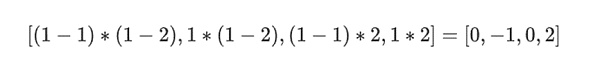
现在我们取这个线性组合 t:
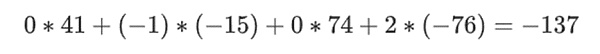
这和直接求多项式的结果是一样的。
以上内容非常接近于对「简单」Binius 协议的完整描述。这已经有了一些有趣的优点:例如,由于数据被分成行和列,因此你只需要一个大小减半的字段。但是,这并不能实现用二进制进行计算的全部好处。为此,我们需要完整的 Binius 协议。但首先,让我们更深入地了解二进制字段。
二进制字段
最小的可能域是算术模 2,它非常小,我们可以写出它的加法和乘法表:
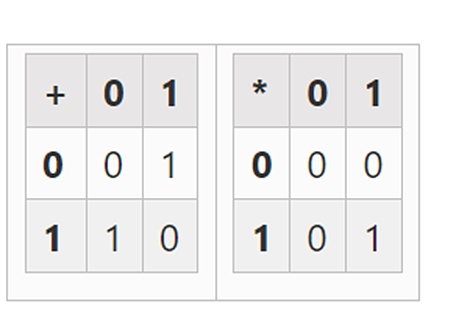
我们可以通过扩展得到更大的二进制字段:如果我们从 F2( 整数模 2) 然后定义 x 在哪里 x 的平方=x+1,我们得到以下的加法和乘法表:
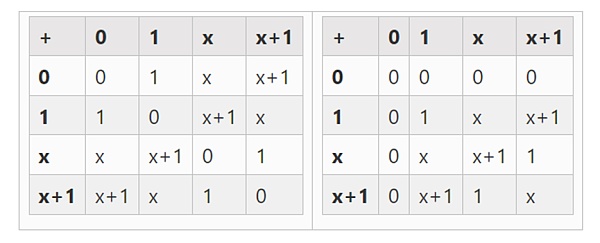
通过塔式结构扩展二进制字段的新方法
近日,一项新的研究表明,通过一种名为塔式结构的构造,我们可以将二进制字段扩展到任意大的大小。与实数上的复数不同,在实数上,虽然你可以加入新的元素,但却无法进一步添加元素 I (四元数的存在不容忽视,但在数学上它们相当奇特,比如:ab 不等于 ba)。而通过有限的字段,我们却可以不断添加新的扩展。具体来说,我们对元素的定义如下:
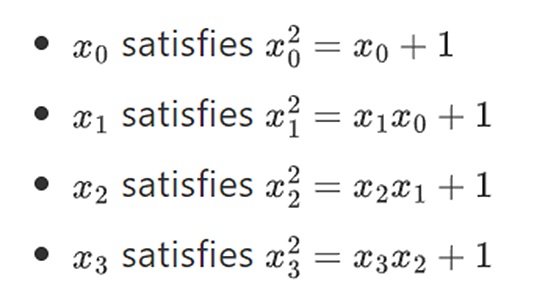
不过话说回来……。这种结构通常被称为塔式结构,因为每一次连续的扩展都好比给塔增加了一层。虽然这并非构造任意大小二进制字段的唯一方法,但它却具有一些独特的优点,而 Binius 正是充分利用了这些优点。
我们可以将这些数字表示为 bit 的列表。例如,1100101010001111。其中,第一位表示 1 的倍数,第二位表示 x0 的倍数,而后续位则依次表示以下 x1 数的倍数:x1、x1*x0、x2、x2*x0,依此类推。这种编码之所以优秀,是因为它可以被分解:
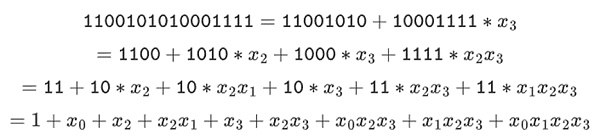
尽管这种表示相对较少见,但我个人倾向于将二进制字段元素表示为整数,并采用更有效的方式将 bit 放在右侧进行表示。也就是说,1=1,x0=01=2,1+x0=11=3,1+x0+x2=11001000 =19,依此类推。在这个表达式中,结果是61779。
在二进制字段中,加法仅仅是异或操作(同样,减法也是如此);值得注意的是,这意味着对于任何 x,x+x=0。而将两个元素 x*y 相乘,则有一个非常简单的递归算法:将每个数字分成两半:
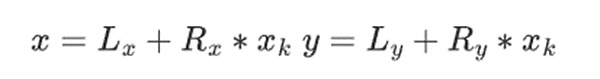
接下来,我们将乘法进行拆分:
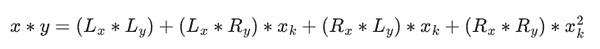
最后一部分略微棘手,因为你需要应用简化规则。虽然有更有效的乘法方法,类似于 Karatsuba 算法和快速傅里叶变换,但我将其留给有兴趣的读者作为练习。
在二进制字段中,除法通过结合乘法和反转来完成。最简单但较慢的反转方法是应用广义费马小定理。但也存在一种更复杂但更有效的反演算法,你可以在此处找到。同时,你也可以在这里找到代码来实践二进制字段的加法、乘法和除法。
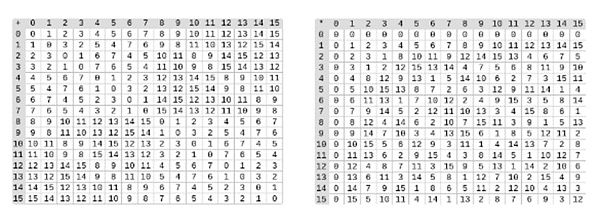
△ 左图:四位二进制字段元素(即仅由 1、x0、x1、x0x1)的加法表。右图:四位二进制字段元素的乘法表。
这种类型的二进制字段之所以令人惊叹,是因为它结合了「正则」整数和模运算的一些最优秀的部分。与正则整数类似,二进制字段元素是无限的:你可以随意扩展。但与模运算一样,如果你在一定范围内进行值的运算,那么你所有的结果也将保持在相同的范围内。例如,如果取 42 连续幂,则结果为:

255 步之后,您回到 42 的 255 次方=1,就像正整数和模运算一样,它们遵循通常的数学定律:a*b=b*a、a*(b+c)=a*b+a*c,甚至还有一些奇怪的新法律。
最后,二进制字段可以方便地处理 bit:如果您用适合 2 的 k 次方的数字做数学运算,那么您所有的输出也将适合 2 的 k 次方 bit。这避免了尴尬。在以太坊的 EIP-4844 中,一个 blob 的各个「块」必须是数字模 52435875175126190479447740508185965837690552500527637822603658699938581184513,因此编码二进制数据需要扔掉一些空间,并在应用层进行额外的检查,以确保每个元素存储的值小于 2 的 248 次方。
这也意味着二进制字段运算在计算机上是超级快的——无论是 CPU,还是理论上最优的 FPGA 和 ASIC 设计。
这一切都意味着我们可以像上面所做的 Reed-Solomon 编码那样做,以一种完全避免整数「爆炸」的方式,就像我们在我们的例子中看到的那样,并且以一种非常「原生」的方式,计算机擅长的那种计算。二进制字段的「拆分」属性——我们是如何做到的 1100101010001111=11001010+10001111*x3,然后根据我们的需要进行拆分,这对于实现很大的灵活性也是至关重要的。
完整的 Binius
有关该协议的 python 实现,请复制下方链接到浏览器查阅:https://github.com/ethereum/research/blob/master/binius/packed_binius.py
现在,我们可以进入「完整的 Binius」,它将「简单的 Binius」调整为 (i) 在二进制字段上工作,(ii) 让我们提交单个 bit。这个协议很难理解,因为它在查看比特矩阵的不同方式之间来回切换;当然,我花了更长的时间来理解它,这比我通常理解加密协议所花的时间要长。但是一旦您理解了二进制字段,好消息是 Binius 所依赖的「更难的数学」就不存在了。
这不是椭圆曲线配对,在椭圆曲线配对中有越来越深的代数几何兔子洞要钻;在这里,您只需要二进制字段。
让我们再看一下完整的图表:

到目前为止,您应该已经熟悉了大多数组件。将超立方体“扁平化”成网格的思想,将行组合和列组合计算为评价点的张量积的思想,以及检验“Reed-Solomon 扩展再计算行组合”和“计算行组合再 Reed-Solomon 扩展”之间的等价性的思想,都是在简单的 Binius 中实现的。
“完整的 Binius”有什么新内容?基本上有三件事:
- 超立方体和正方形中的单个值必须是 bit(0 或 1)。
- 扩展过程通过将 bit 分组为列并暂时假定它们是较大的字段元素,将 bit 扩展为更多的 bit。
- 在行组合步骤之后,有一个元素方面的“分解为 bit”步骤,该步骤将扩展转换回 bit。
我们将依次讨论这两种情况。首先,新的延期程序。Reed-Solomon 代码有一个基本的限制,如果您要将 n 扩展到 k*n,则需要在具有 k*n 不同值的字段中工作,这些值可以用作坐标。使用 F2 (又名 bit),您无法做到这一点。因此,我们所做的是,将相邻 F2 的元素“打包”在一起形成更大的值。在这里的示例中,我们一次将两个 bit 打包到 {0,1,2,3}元素中,因为我们的扩展只有四个计算点,所以这对我们来说已经足够了。在“真实”证明中,我们可能一次返回 16 位。然后,我们对这些打包值执行 Reed-Solomon 代码,并再次将它们解压缩为 bit。

现在,行组合。为了使“在随机点求值”检查加密安全,我们需要从一个相当大的空间 ( 比超立方体本身大得多 ) 中对该点进行采样。因此,虽然超立方体内的点是位,但超立方体外的计算值将大得多。在上面的例子中,“行组合”最终是[11,4,6,1]。
这就出现了一个问题:我们知道如何将 bit 组合成一个更大的值,然后在此基础上进行 Reed-Solomon 扩展,但是如何对更大的值对做同样的事情呢?
Binius 的技巧是按 bit 处理:我们查看每个值的单个 bit ( 例如:对于我们标为“11”的东西,即[1,1,0,1] ),然后按行扩展。对象上执行扩展过程。也就是说,我们对每个元素的 1 行执行扩展过程,然后在 x0 行上,然后在“x1”行上,然后在 x0x1 行上,依此类推(好吧,在我们的玩具示例中,我们停在那里,但在实际实现中,我们将达到 128 行(最后一个是 x6*…*x0 ))
回顾
我们把超立方体中的 bit,转换成一个网格,然后,我们将每行上的相邻 bit 组视为更大的字段元素,并对它们进行算术运算以 Reed-Solomon 扩展行。
接着,我们取每列 bit 的行组合,并获得每一行的 bit 列作为输出 ( 对于大于 4x4 的正方形,要小得多 )。
最后,我们把输出看成一个矩阵,再把它的 bit 当作行。
为什么会这样呢?在“普通”数学中,如果您开始将一个数字按 bit 切片,( 通常 ) 以任意顺序进行线性运算并得到相同结果的能力就会失效。
例如,如果我从数字 345 开始,我把它乘以 8,然后乘以 3,我得到 8280,如果把这两个运算反过来,我也得到 8280。但如果我在两个步骤之间插入一个“按 bit 分割”操作,它就会崩溃:如果你做 8 倍,然后做 3 倍,你会得到:

二进制场中的新方法
在最新的技术研究中,一种全新的方法正在被探索,以提高二进制场的构建效率。研究发现,通过特定的乘法运算,可以显著提高效率。
例如,假设你连续进行了 3 倍和 8 倍的操作:
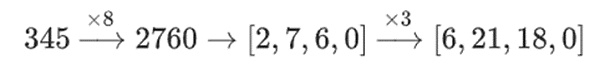
虽然一般的数学运算可能不起作用,但在采用塔结构构建的二进制场中,这种方法却十分有效。这是因为二进制场具有可分离性:当你将一个大值乘以一个小值时,每个线段上的结果都会保留在该线段上。
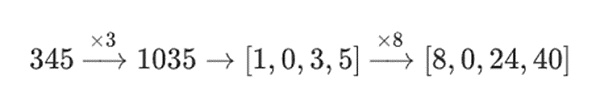
随后,对每个分量进行相同的 11 倍操作。
将它们整合在一起
此外,研究人员指出,零知识证明系统的工作原理涉及对多项式进行陈述,并同时表示底层评估的陈述。以斐波那契计算为例,通过 F(X+2)-F(X+1)-F(X) = Z(X)*H(X) 这样的陈述,同时检查所有斐波那契计算步骤。他们通过在随机点进行证明求值来检查多项式的陈述。
然而,在实践中,研究人员发现效率低下的主要原因之一是处理的数字通常较小,如 for 循环中的索引、True/False 值等。为了解决这个问题,研究人员正在尝试使场尽可能小,以减少额外的开销。
最新的研究成果表明,使用二进制场可以更好地处理这一问题。相比之下,Reed-Solomon 编码通常会导致较大的冗余,占用更多的空间。
因此,Plonky2 和 Plonky3 等新方法将数字大小降至最低,从而提高了效率。通过使用二进制字段,研究人员可以更加密集地编码数据,从而减少额外开销。
总的来说,这些新方法为提高二进制场的构建效率提供了新的途径,为未来的技术发展带来了希望。

以上为本次新闻稿的相关内容,感谢您的阅读。
Binius发布新闻
Binius致力于开发一种多项式承诺方案,它可以证明在一个超立方体 P(x0,x1,…xk) 上的单个计算点 P(0,0,0,0) 到 P(1,1,1,1) 的数值。然后,通过将相同的数据重新解释为一个平方,并使用Reed-Solomon编码扩展每一行,以提供数据冗余,以满足随机Merkle分支查询的安全需求。接下来,我们计算行的随机线性组合,设计系数,确保新的组合行包含我们关心的计算值。验证者可以通过传递这些新创建的行(被重新解释为128行位)和一些随机选择的带有Merkle分支的列来验证这些数据。
验证者还会执行对“扩展的行组合”(或者说是扩展的几列)和“行组合的扩展”进行验证是否匹配。接着计算一列组合,并检查其返回值是否与证明者声明的值相匹配。这就是我们的证明系统(多项式承诺方案的核心组成部分)。
我们还需要解决哪些问题?
-
快速傅里叶变换在二进制字段上的有效算法。这在提高验证者计算效率方面至关重要。我们在论文中描述了这一技术,但确切的实现可能会有所不同。
-
一元多项式的算术化。Binius提出了解决方案,但其中仍存在一些挑战。
-
如何安全地进行特定值检查。我们尚未讨论如何应对已知计算检查的安全性。
-
查找协议和超高效证明系统的结合应用。这是另一个需要解决的挑战。
-
超越平方根验证时间。Binius证明的bit大小令人头疼,我们需要寻找其他证明系统来弥补这一问题。
-
Binius对“SNARK友好”的影响。使用Binius后,不再需要担心如何使计算“算术友好”。这是一个复杂的话题,需要进一步探讨。
我们期待在未来几个月里,基于二进制字段的证明技术能够有更多进展。
```
注册有任何问题请添加 微信:MVIP619 拉你进入群

打开微信扫一扫
添加客服
进入交流群
1.本站遵循行业规范,任何转载的稿件都会明确标注作者和来源;2.本站的原创文章,请转载时务必注明文章作者和来源,不尊重原创的行为我们将追究责任;3.作者投稿可能会经我们编辑修改或补充。





 = -137。在这里,我们只使用一半评估坐标的偏张量乘积相乘,并将 N 值网格简化为一行根号 N 的值。如果你将此行提供给其他人,他们可以使用另一半求值坐标的张量积来完成剩余的计算。</p>
<p style=)












